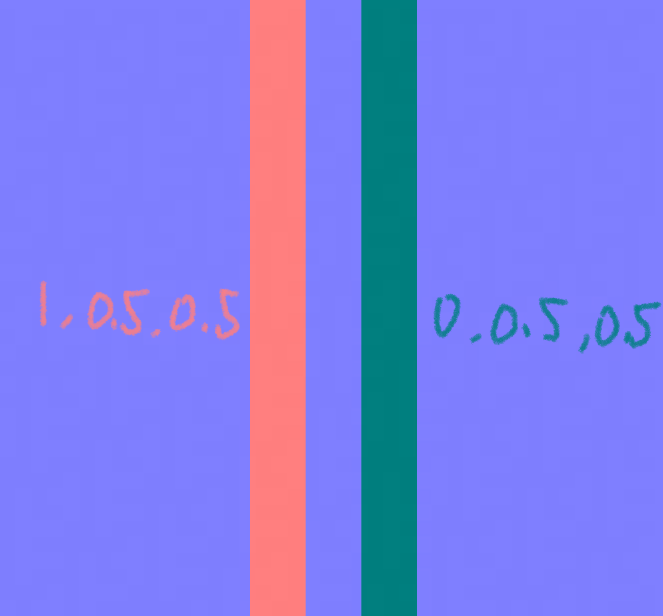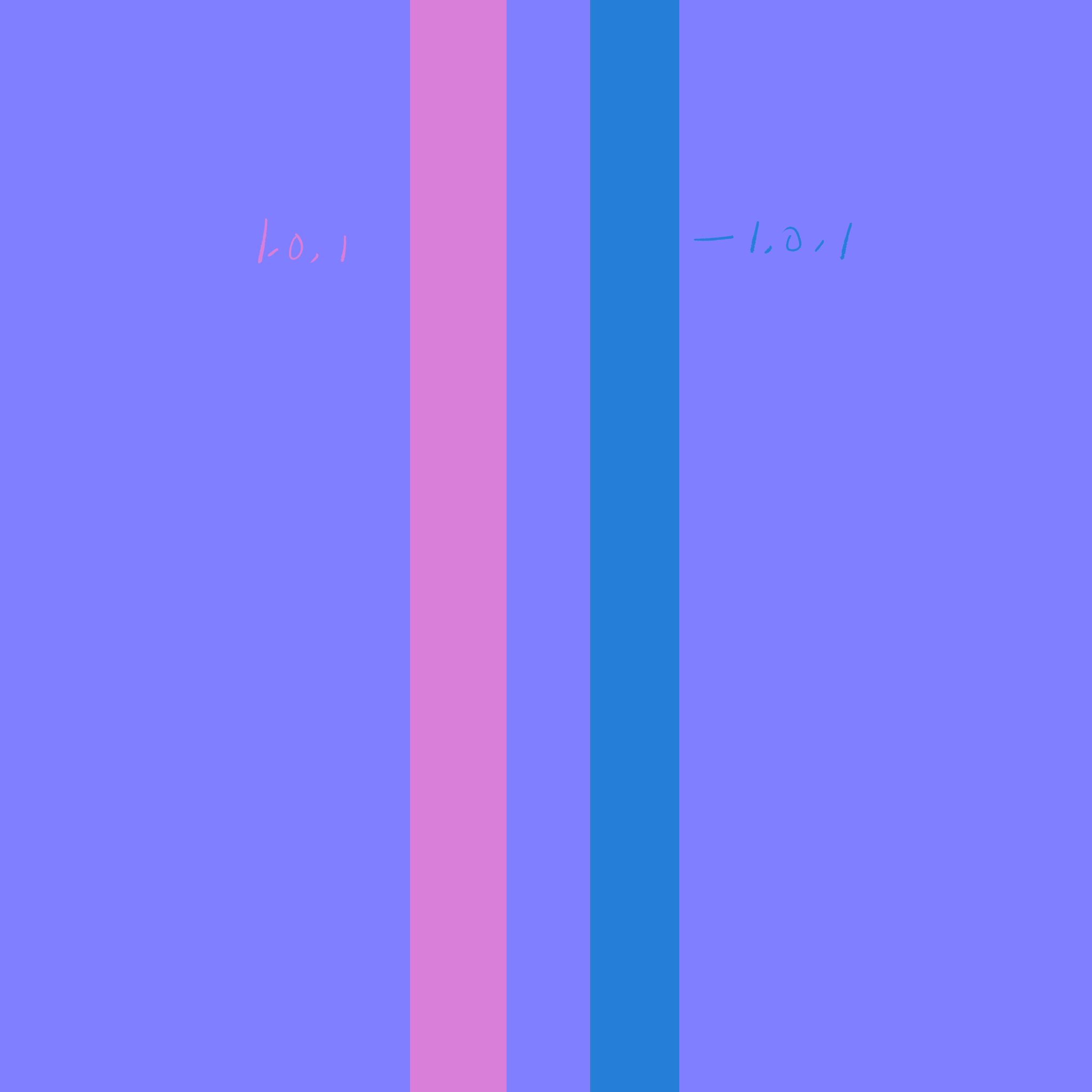法线贴图是用来干什么的?
之前听过一个说法,给我留下了比较深刻的印象:法线贴图就是用来偏移原本的法线的。
实际上这个说法并不完全正确,今天就是要来矫正一下我对法线贴图的误解。
法线贴图是用来设置法线的,就和baseColor是用来设置颜色的一样。其过程是“等于”(n=tex)而不是“加等于”(n=n+tex)。
从效果上来看确实是使原本的法线发生了偏移,这是因为赋值的过程在切线空间中发生,而切线空间的核心定义之一就是原本的法线。
手搓法线贴图
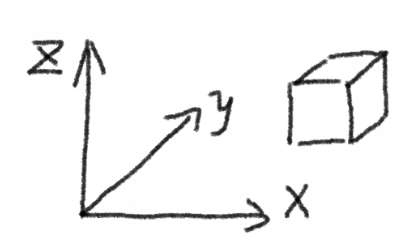
首先我们来定义一个坐标系,就是大家初中学过的那个。没有坐标系,世界就是混沌的。 有了之后,我就可以说(1,1,1)代表的是一个朝向右-前-上方向,和水平面夹角为45°的向量。
把这个颜色填满画布,就得到了一张默认的法线贴图-大家最喜欢的蓝紫色。
为什么默认情况下是蓝紫色呢?
默认情况下,法线应该是朝上的:(0,0,1)。
向量被压缩到贴图中,需要(➕1),(➗2),这样做是为了区分正负(贴图中是没有负值的),你可以用(0.3,0.3)的贴图来表示(-0.4,-0.4)这个方向。(0,0,1)最后进入贴图变成(0.5,0.5,1),也就是蓝紫色。
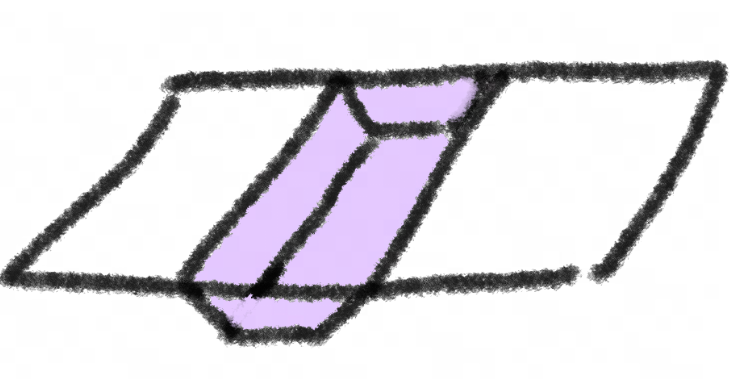
好的,我现在希望这个法线贴图能表现一个竖着(Y方向)的凹槽
那么我就额外需要两个向量:一个向着右上方,一个向着左上方,分别代表凹槽的两个斜坡
我们先假设这个斜坡是90度角,也就是垂直于平面,那么两个斜坡的法线向量分别为:(1,0,0)(-1,0,0)
将他们压缩到贴图中,就变成了(1,0.5,0.5)(0,0.5,0.5)
好像有点太过了,毕竟一个小凹槽并不会有直角一样的转折,那么,我再加工一下,把它变成45度角吧。
需要的向量是:(1,0,1)(-1,0,1)
将他们单位化:我们只需要方向就行了,不需要长度,过长的长度会在我们(➕1),(➗2)后超出贴图的最大范围(0-1),导致失真。
以(1,0,1)为例,得到:(1/√2,0,1/√2 )≈(0.7,0,0.7),转化为贴图即是(0.85,0.5,0.85)
凹还是凸?
人眼到底是怎么鉴别凹凸的呢?
我们来看看这张图
这个地方是突起的还是凹陷的呢,其实两者都有可能,假设右上方是光线的来源,则这个图就是突起的,左下方是光照的来源,则这个地方就是凹陷的。
有了参照物,也许我们能够更好理解这一点。(但你也可以把这张图理解成左右两边都有打光的情况下,中间凸起来)
我们在一些条件下能够很快判断突起和凹陷,其实是人脑自动分析环境光影的结果——光照打过来,迎着光的角度会变得更亮,背光的角度会变得更暗。
如果我们给大脑不够充分的信息,很容易就能形成视错觉。
大脑通过什么来判断凹和凸 - 视错觉实验室
《Making Up the Mind》上讲了这么一个简单但深刻的实验:
我们看到这张图片的第一反应是:5个凸的按钮,1个凹的按钮。
现在仅仅将图片上下颠倒一下:
在我们眼中立即就变成了:1个凸的按钮,5个凹的按钮。
为什么同一副图片,仅仅是上下颠倒一下,我们就对其作出了完全不同的解释呢?
我们知道,视觉图像要到达大脑,首先要在视网膜上成像(视网膜上密密麻麻地排布着感光细胞),刺激感光细胞形成的神经电冲动然后经过一系列复杂的神经通路到达视觉皮层。但后续的繁杂步骤其实都是对视网膜上成的像的处理。这里,对我们的讨论而言视网膜不妨可以看作一张感光胶片,重点在于视网膜上的像完全是一张二维图片。大脑从图像中提取出来的任何信息都以这张二维图片为原始素材。
那么,究竟大脑是怎么从二维图片中看出(推导出)三维的?
其中一个重要的工作就是判定深度。前面的两张图片完全是二维图片,在我们的视网膜上也是二维的。然而大脑却能够从中理解出三维出来,大脑能够判断出一个按钮是“凹”的还是“凸”的。这是怎么办到的?
很简单,假设环境中有光源,并且光源来自上方,那么凸的物体会使其下部出现阴影,凹陷的物体则会在上部出现阴影。于是,图中按钮的下半部出现阴影就意味着按钮是凸的,按钮的上半部出现阴影则代表按钮是凹的。
然而,别忘了,大脑的这个推理成立必须有一个前提,即光线从上方照下来,如果光线从下方照下来的话,一切就反过来了,凸的物体将会使其上部呈现阴影,凹的物体将会使其下部呈现阴影。因此同样的一副图片如果假设光线从下方照耀的话,原来看成凸的物体就应该看成凹的,原来看成凹的就应该看成凸的。
那么,回到我们的第一副图片,你能够看着第一副图片并假想光线从下方照下来,进而把原来凸的按钮看成凹的吗?事实证明这很难,但我们可以做一个等价的事情——将图片上下颠倒一下:考虑到我们总是假设光线从上方照耀以及按钮的上下对称性,颠倒原图就相当于对原来的图片而言假设光线从“下方”照上去了。
我们发现(上文第二张图),一旦颠倒图片之后,果然凹凸就换位了。
这就是说,同一副图片其实有两种(乃至更多)可能的解释,取决于你的大脑到底假定光照来自下方还是上方。但为什么我们看上面两幅图片却不会出现“二义性”的错觉呢?因为在我们生存的环境中始终就有这么一个巨大的来自上方的光源——太阳,漫长的进化已经在我们的神经回路中刻下了“光源来自上方”这样一个强大的假设,所以虽然第一副图片本该完全有两种解释,我们还是不可避免地只看到其中的一种解释,即假设光线来自上方的解释,即使卯足了劲看也难以将凸的看成凹的,因为难以克服进化印刻在大脑中的“光线来自上方”的假设,因此为了让你看到“当光线来自下方时你会看到什么景象”我不得不将图片颠倒一下,结果你就看到原来凸的变成凹的了。
对于了解贝叶斯方法的同学,这个“光线来自上方”的假设就是先验(prior)的。
世界在我们眼中其实只是一张二维图片,由于引入了“光照来自上方”这个先验假设,便有了凸凹。否则,文中一开始那张图片中的“按钮”可以是凸的,也可以是凹的,也可以是一张平面的、故意捉弄你的眼睛的画。
最后,我们再来做一个实验,将原图转动90度:
是不是发现凸凹感基本消失了?现在图片看上去更像是透过面板上的一些孔洞看背后的一张黑白条纹纸。前面提到,我们的大脑通过阴影来判断凸凹,在对阴影的“含义”进行推断的时候必须假定光照来自上方,而在这张竖着的图中,假设光照来自上方的话,那些阴影是没有意义的,因为不管凸还是凹,都不会形成这样的阴影,因此我们的大脑便无法判断凸凹了。(注:其实只要稍微把头往某个方向转一下就会看到凸凹了,并且,由于90度的偏角远小于上下颠倒,所以可能不少人还是能够在上图中看出凸凹感来的,只要想象光线来自左方或右方即可,比想象光线来自下方容易多了)。
反转法线贴图的效果
现在我们知道了,(光照不变的情况下,或者不够明确,甚至在一些已经明确的情况下)只要反转一个轴向,就能让人觉得凹凸相反了——事实上也是这样的。
上面用到的这张图,就是我把法线贴图沿着y轴反转了一下(x变换为-x),得出的两个槽,从法线角度来分析,也确实让他们的朝向变得凹凸反转。
(黑色是平面参考线,不用在意具体轴向)

如果阳光是平行于这两个槽的,并且你也以平行的视角去看,则会看到这样的结果
他们光照表现完全相同——这是因为我们只反转了x轴。
OpenGL与DirectX
我曾经搜过几次gl和dx之间法线贴图的区别,得到了这样的回答:
现在看来,也可以解释为什么说“法线贴图是凸出还是凹陷的”了。
为什么我们会觉得,GL的法线是突出的呢?
绿色会显得亮度更高,蓝色会显得亮度更低。那么我们套用光从上面来这个人类的认知习惯,就可以知道gl的法线贴图,上方是迎光的亮面,下方是背光的暗面。
不信的话你可以试试,想着光是从下方打过来的,再去看这张图。
根据上面反转X轴的实验,我们现在也知道了,OpenGL与DirectX的法线为什么看上去效果会反转,就是因为Y轴向相反了。
Unity的计算&反转凹凸
要聊到法线贴图是怎么在模型上生效的,就不得不谈到切线空间。
如果你对图形学已经有一定认识,相信你已经比我更加了解切线空间。
如果你听都没听过切线空间四个字,或者懒得去自己找,那我可以不负责任的告诉你:在我们手搓法线贴图的时候,定义的坐标系就是切线空间。我们的法线贴图,就是在类似这样的坐标系下面进行运算的。一个立方体的每个面都可以看作是有自己的切线空间,每个空间的z轴都和这个面垂直——也就是原本的法线。
简单来说切线空间就是属于每个面自己的,朝上的空间。
之前的这张图就可以看作是很多切线空间,蓝色的是法线,也是空间的z轴。
当我们采样法线贴图的时候,会在切线空间中进行计算,也就是用物体表面的坐标系去赋值法线朝向。这样就算我用相同的贴图(假设是一张表示全部朝上的纯蓝紫色贴图)我们立方体的六个面都可以表现正常——法线没有变化,而不是将所有面的法线都变成朝上(如果你用世界空间计算就会这样)。
这个空间就是靠Mesh.tangents和Mesh.normals去计算出来的。
由上图可知,Mesh.tangents的xyz分量是切线空间的U(X)方向矢量,将xyz与法线叉乘即可得到垂直于这两个方向的副切线[Bitangent](和图中的副法线[Binormal]是一样的,两个叫法而已),且这个副切线理论上朝向Y(垂直)方向。
当我们切换Mesh.tangents的w值时,其垂直方向的副切线会反转,也就是从OpenGL变成DirectX(反过来说也成立)。
附上代码一段
void Reverse()
{
MeshFilter filter = GetComponent<MeshFilter>();
if (filter != null)
{
Mesh mesh = filter.sharedMesh;
Vector4[] tangents = mesh.tangents;
for (int i = 0; i < tangents.Length; i++)
{
tangents[i] = new Vector4(tangents[i].x, tangents[i].y, tangents[i].z, -tangents[i].w);
}
mesh.tangents = tangents;
}
}